System Memory: Stack vs Heap Tutorial

System memory: Stack vs Heap

Before we continue with the tutorial series, let’s take a quick look at the basics of the stack and the heap in memory.

We already know that while a program is running, it stores data such as variables or classes temporarily in memory (RAM).

Memory is separated into two areas. There is a portion of the memory called the Stack, and that’s where local variables are allocated.

Then there is a portion of the memory called the Heap and that’s where class instances are allocated.

As an example, let’s use the following class.

namespace Memory
{
    class Program
    {
        static void Main(string[] args)
        { }

        class Person
        {
            public string name;
            public int age;
        }

    }
}

When we declare a variable of type Person in the Main() function.

namespace Memory
{
    class Program
    {
        static void Main(string[] args)
        {
            Person p;
        }

        class Person
        {
            public string name;
            public int age;
        }

    }
}

It doesn’t mean we allocate enough space for the class members name and age. It means, allocate enough space for a reference to a Person. So, Person p only declares a variable.

Space to store that variable is allocated on the stack. Initially it’s undefined, that’s to say it has no value, it’s just random bits.

If we were to try and modify the name member.

namespace Memory
{
    class Program
    {
        static void Main(string[] args)
        {
            Person p;
            p.name = "John";
        }

        class Person
        {
            public string name;
            public int age;
        }

    }
}

The compiler would raise an error because it detected that we haven’t set p equal to anything. p is not a Person on the heap so we can’t access its member.

Allocate with new

Now, let’s compare this use of variables of type Person with actually allocating a Person.

We allocate all the space needed for the members of Person on the heap by calling the new operator.

namespace Memory
{
    class Program
    {
        static void Main(string[] args)
        {
            new Person();
        }

        class Person
        {
            public string name;
            public int age;
        }

    }
}

Now we get enough space on the heap for a reference to the members name and age.

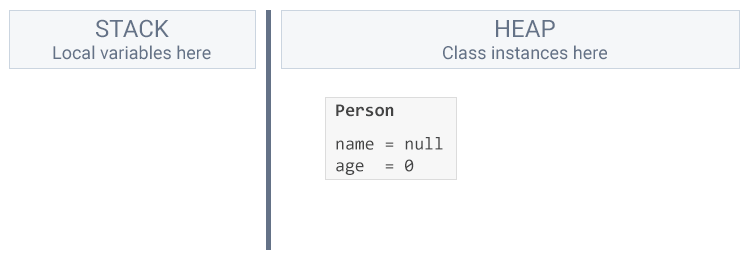
At the moment we can’t do anything with Person even though it’s allocated on the heap. We have to store a reference to this Person to be able to use it.

namespace Memory
{
    class Program
    {
        static void Main(string[] args)
        {
            Person p;
            p = new Person();
        }

        class Person
        {
            public string name;
            public int age;
        }

    }
}

Now we have the variable p on the stack pointing to a Person on the heap.

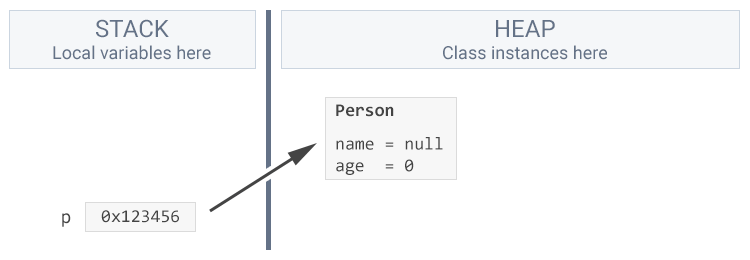
As we’ve seen we can shorten this procedure into one line.

namespace Memory
{
    class Program
    {
        static void Main(string[] args)
        {
            Person p = new Person();
        }

        class Person
        {
            public string name;
            public int age;
        }

    }
}

Now that we’ve allocated a new person on the heap, and have a variable on the stack pointing to it, we can access the members on that Person.

namespace Memory
{
    class Program
    {
        static void Main(string[] args)
        {
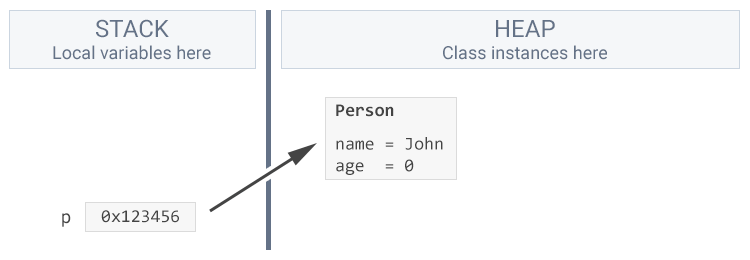
            Person p = new Person();
            p.name = "John";
        }

        class Person
        {
            public string name;
            public int age;
        }

    }
}

Multiple allocations

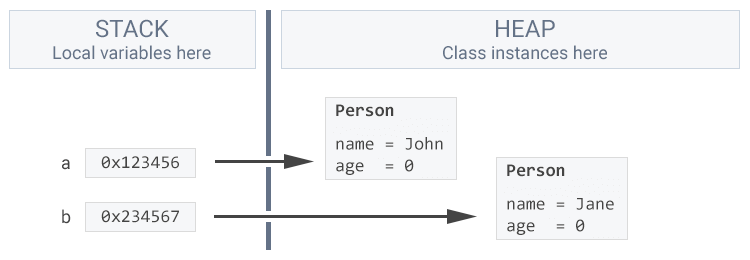
We can create more people and give each its own variable that points to the allocation on the heap.

namespace Memory
{
    class Program
    {
        static void Main(string[] args)
        {
            Person a = new Person();
            a.name = "John";

            Person b = new Person();
            b.name = "Jane";
        }

        class Person
        {
            public string name;
            public int age;
        }

    }
}

Overwrite an allocation

What happens if we “overwrite” the variable that’s pointing to a Person with a new Person?

namespace Memory
{
    class Program
    {
        static void Main(string[] args)
        {
            Person p = new Person();
            p.name = "John";

            p = new Person();
            p.name = "Jane";
        }

        class Person
        {
            public string name;
            public int age;
        }

    }
}

The p variable will now point to the new Person, “Jane”. We’ve lost the reference to the old Person, “John”. We have no way of accessing it anymore.

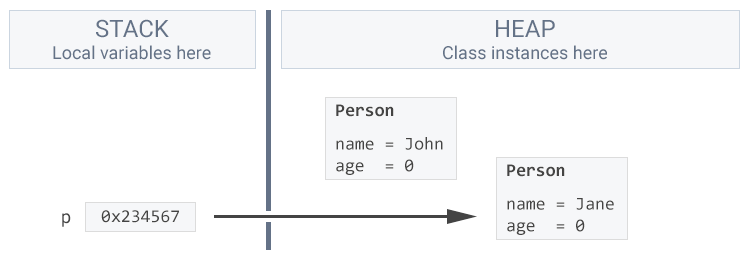
At some point in the future the garbage collector will come and remove the Person “John” from the heap to free up space.

Because nothing points to “John”, the garbage collector assumes that he isn’t used and is available to be removed.

Copy from stack to heap

Primitive types, otherwise known as value types in .NET, are allocated on the stack. One such example would be an int.

namespace Memory
{
    class Program
    {
        static void Main(string[] args)
        {
            int age = 30;
        }

        class Person
        {
            public string name;
            public int age;
        }

    }
}

If our variable has no value it will be allocated with random bits. In this case though our variable does have the value of 30.

When we assign a local variable to a class member the value is copied.

namespace Memory
{
    class Program
    {
        static void Main(string[] args)
        {
            int age = 30;

            Person p = new Person();
            p.name = "John";
            p.age = age;
        }

        class Person
        {
            public string name;
            public int age;
        }

    }
}

What happens here is that the value of the local variable age is copied from the stack into p.age in the heap.

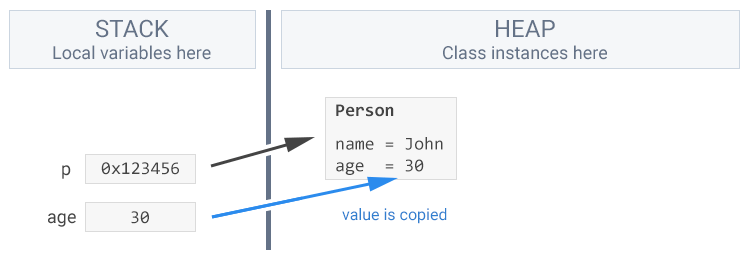
There exists no connection between age and p.age because the value has been copied, not moved. If we were to change the local variable age, it would have no impact on the member variable p.age.

using System;

namespace Memory
{
    class Program
    {
        static void Main(string[] args)
        {
            int age = 30;

            Person p = new Person();
            p.name = "John";
            p.age = age;

            age = 50;

            Console.WriteLine("Class instance p.age: " + p.age);
            Console.WriteLine("Local variable age after value change: " + age);
            Console.ReadLine();
        }

        class Person
        {
            public string name;
            public int age;
        }

    }
}

Summary: Points to remember

• System memory is separated into two areas, the stack and the heap.
• Value types, like local variables, are stored in the stack.
• Reference types, like class instances, are stored in the heap.
• When we use the new keyword, we allocate space on the heap.
  • Before members can be accessed, we must create a reference on the stack that points to the allocation on the heap.
• When we overwrite a reference from the stack to point to a new allocation on the heap, we won’t have access to the previous reference.
  • At some point in the future, the garbage collector will come and clean up the unlinked reference.
• When we assign a local variable to a class member the value is copied.
  • The local variable will not have any connection to the class member.